Bandgap Physics
J. C. Daly
December 1, 2005
The voltage drop across a pn junction carring the
current, I is,
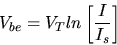
| (1) |
where VT is the thermal voltage.
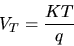
| (2) |
Is depends on temperature,
physical constants and fabrication parameters.
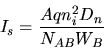
| (3) |
where A is the emitter area, q is the electronic
charge, Dn is the diffusion constant for electrons,
NAB is the acceptor doping in the base, and
WB is the width of the base.
mn is the electron mobility
in the base.
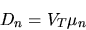
| (4) |
The temperature dependence of mobility depends on doping.
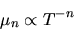
| (5) |
where n is 1.5 in lightly doped silicon and n is -1.5 in heavily
doped silicon. In the lightly doped transistor base n may be about 1.
ni , the intrinsic carrier concentration,
is strongly temperature dependent.
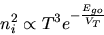
| (6) |
where Ego is the silicon bandgap voltage
extrapolated to 0 oK.
Plugging Equations 4, 5, and 6 into Equation 3 results in the
following temperature dependence of Is.
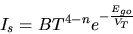
| (7) |
where B is a temperature independent constant.
Plugging Equation 7 into Equation 1,and assuming 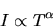 ,
,
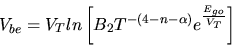
| (8) |
where B2
is a temperature independent constant.
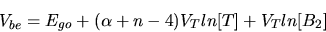
| (9) |
The output voltage is the sum of Vbe that decreases
with temperature and a voltage proportional to VT
that increases with temperature, since VT is
proportional to the absolute temperature, T.
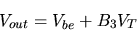
| (10) |
where B3 is a temperature independent constant.
Plugging Equation 9 into Equation 10,
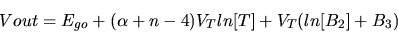
| (11) |
The desired bandgap output is to a first order independent of
temperature. Taking the derivative of
Vout,
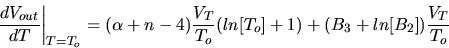
| (12) |
Setting the derivative of Vout with
respect to temperature equal to zero.
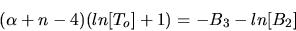
| (13) |
Using Equation 13 to eliminate B2
and B3 from Equation 11,
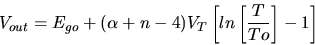
| (14) |
For example
If
then.
Vout = Ego + 2 VT
Since Ego = 1.205V,
Vout = 1.25 V
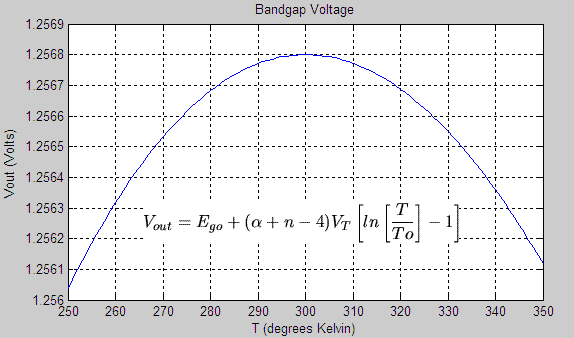
Figure 1 The bandgap output voltage (Rainbow curve) is shown,
where n = 1,
a = 1, VT = KT/q, To = 300,
and
Ego = 1.205V.
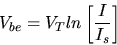
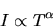 ,
,
